-
重心是三角形三条中线的交点。有以下性质:1、三角形的重心到顶点的距离是他到对边中点的距离的2倍;2、三角形的重心与各个顶点连线组成的三角形面积相等并且等于原三角形面积的13;3、如果经过三角形顶点和重心到直线垂直对边,三角形是等腰三角形。利用勾股定理还可以推出重心的其他性质。
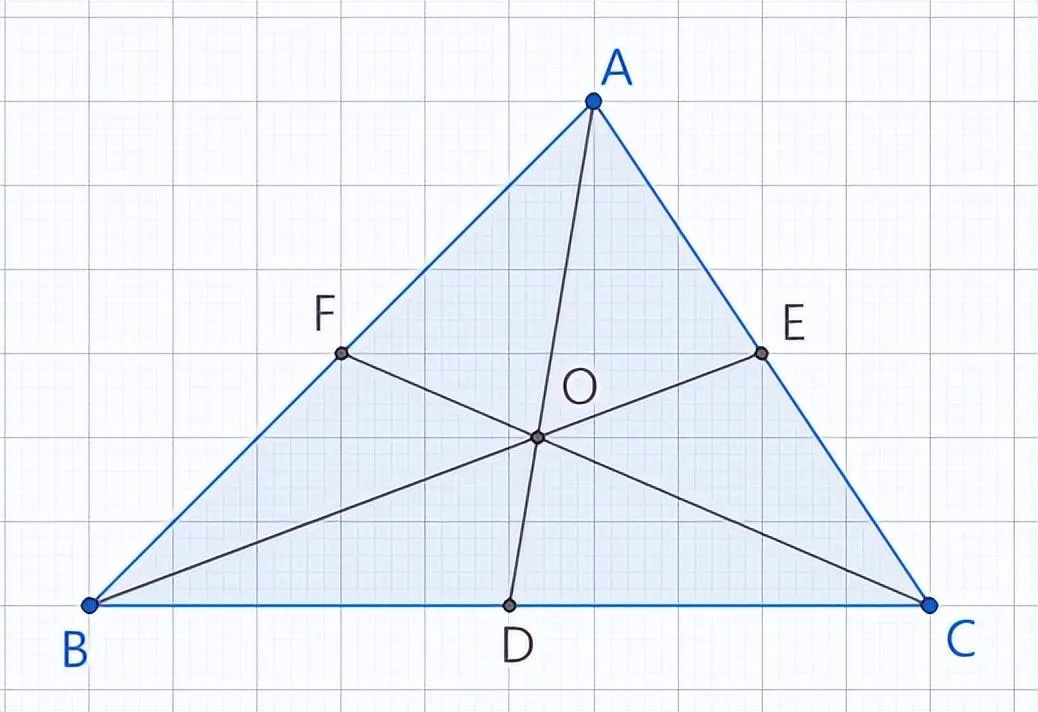
三角形重心是三角形三条中线的交点,是一个非常特殊的点,具有很多特殊的性质。有些涉及重心的问题,直接使用这些性质会事半功倍。下面简要总结一下。
1.三角形重心到顶点的距离与重心到对边中点的距离之比为2:1
△ABC中,AD、BE、CF分别为BC、AC、AB边上的中线,交点为O。则AO:OD=BO:OE=CO:OF=2:1
证明:
如图,连接EF与AD交于G,由三角形中位线定理知,EF∥BC。又因E为AC中点,因此G是AD中点。
因为△EOG∽△BOD,且相似比为1:2,因此可计算出:
AG:GO:OD=3:1:2,于是AO:OD=2:1。其他同理。
这个定理在一些给出重心要求计算边长关系的问题中相当有用。
2.三角形的重心和三个顶点组成的三个三角形面积相等
△ABC中,AD、BE、CF分别为BC、AC、AB边上的中线,交点为O。则S△AOB=S△BOC=S△COA
证明:先证S△AOB=S△BOC,其他同理。
(计算三角形面积基本上要做“高”的辅助线)
因为△AOB=△BOC同底,因此其面积比等于高长比
过A做AP⊥BE于 P,过C做CQ⊥BE延长线于Q。
因E是AC中点,AE=CE,由AAS定理易得△AEP≌△CEQ
因此AP=CQ
S△AOB:S△BOC=AP:CQ=1,因此S△AOB=S△BOC
3.三角形的重心是三角形内到三边距离之积最大的点。
如图,O是△ABC内一点,O到三条边的距离分别为h₁、h₂、h₃。
求证:当O为△ABC的重心时,h₁•h₂•h₃取最大值
证明:设三角形三条边长分别为a、b、c,连接AO、BO、CO。
S△ABC= S△AOB+ S△BOC+ S△COA =1/2(a•h₁+b•h₂+c•h₃)
给定了△ABC,那么S△ABC是定值,三边长a、b、c也是定值。
变化的是O的位置,也就是h₁、h₂、h₃是变量。
若求h₁•h₂•h₃的最大值,那么最直观的是使用基本不等式。
利用不等式的思想就是:“将变量向定量上凑”。
因为给定的定量是三角形的边长和面积,那么就要凑出
h₁•h₂•h₃≤X(X是定值)的形式,且一定是朝着
S△ABC=1/2(a•h1+b•h2+c•h3)的方向做变换
积与和之间的基本不等式为:几何平均数≤算数平均数
当有两个变量时,其形式为:
当有三个变量时,其形式为:
于是我们可以得到:
(当且仅当ah₁=bh₂=ch₃时等号成立,等号成立的条件极其重要)
那么,无需继续进行计算,只需要知道当ah₁=bh₂=ch₃时,h₁•h₂•h₃取最大值即可。
那么此时S△AOB=S△BOC=S△COA,即O是重心。
因此,当O为△ABC重心时,到三边距离之积最大。