-
1.如何用excel算t值 百度文库
1、打开excel输入数据,如A组数据和B组数据进行比较,如下图所示;
2、在空格中输入【=】,再插入函数【T-Test】,如下图所示;
3、Array1选择A组数据,Array2选择B组数据,trails和type输入2,如下图所示;
4、点击【确定】,进行T-test分析,如下图所示;
5、分析结果,若P<0.05在存在显著性差异,若P<0.01则存在极显著性差异,如下图所示。
2.一些数据可以求出T值,我要怎么才能求的P
菜鸟求教怎么看t值和p值
t值和P值都用来判断统计上是否显著的指标。
p值就是拒绝原假设的最小alpha值嘛,把统计量写出来,带进去算出来之后,根据统计量的分布来算p值啊,举个例子,比如说算出来的统计量的值为z,服从的是正态分布,如果是双边检验的话那么pvalue=2*(1-probnorm(abs(Z)));
单边检验的话,应该是1-probnorm(z);
具体问题具体分析,不同的检验方法求p值方法也不一样,统计的书上肯定都有;T值计算方法相似。
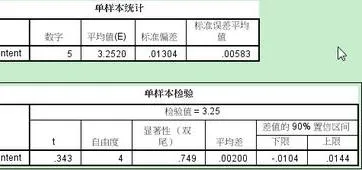
3.两个均数已计算出怎样用SPSS计算t值和P值
1、首先打开要进行配对设计样本均数的比较的数据表。
2、然后选择【分析-比较均值-配对样本T检验】。
3、接着将要配对的两个变量拖到成对变量框中。
4、选择【选项】,然后置信区间调整为95%。
5、再点击【bootstrap】,将执行bootstrap取消。
6、最后即可看到结果,P值小于0.05,可以认为配对样本有统计学差异。
4.已知标准差,平均值,列数怎么算的p值和t值
已知样本的标准差和平均值,可以求出t值。P值是指由H0成立时的检验统计量出现在由样本计算出来的检验统计量的末端或更末端处的概率值。通过查t界值表,得到P值的范围。
t检验是用于两个样本(或样本与群体)平均值差异程度的检验方法。它是用t分布理论来推断差异发生的概率,从而判定两个平均数的差异是否显著。分以下三种情况:
1、单个样本与总体均数的比较
单样本t检验用于比较样本数据与一个特定数值之间是否的差异情况。
2、配对设计的t检验
研究的是差值均数(样本均数)与理论上的差值总体均数的比较。 首先计算出各对差值d的均数。当两种处理结果无差别或某种处理不起作用时,理论上差值d的总体均数μd=0。可将配对设计资料的假设检验视为样本均数与总体均数μd=0的比较。
其中 d是差值的样本均值,s是差值的样本标准差。
3、两个独立样本均数的比较
计算公式如下图所示,其中 x1和 x2 分别是两组样本的样本均值, n1 和 n2 分别是两组样本的大小,s1 和 s2 分别是两组样本的样本标准差。
扩展资料:
1、t检验的适用条件为样本分布符合正态分布。 t检验的应用条件:
当样本例数较小时,要求样本取自正态总体;
做两样本均数比较时,还要求两样本的总体方差相 等。
2、t检验有多种类型,可以分为只有一组样本的t检验和有两组样本的t检验。
(1)单样本t检验用于检验样本的分布期望是否等于某个值。
(2)双样本t检验用于检验两组样本的分布期望是否相等,又分为配对t检验和非配对t检验。
配对t检验的两组样本数据是一一对应的,而非配对t检验的两组数据则是独立的。比如药物实验中,配对t检验适用于观察同一组人服用药物之前和之后,非配对t检验适用于一组服用药物而一组不服用药物。
参考资料:
百度百科——t检验
5.如何用excel计算p值
P(T<=t)
单尾
9.71817E-49
P(T<=t)
双尾
1.94363E-48
这就是P值啊,9.71817E-49就是9.71817*10^(-49),这个P值很小,是拒绝原假设的P值
1、打开excel表格,输入需要的两组数据。
2、选择一个空白表格,选择函数fx,类别选择:统计。
3、选择TTEST,点击第一组数值,拖动鼠标把第一组方框数据选中。同样点击第二组数值选中第二组方框数据。
4、尾数和类型都输入“2”,点击确认即可。如果P小于O.01,说明这两组数据是极显著差异性。
5、如果P值0.01-0.05说明这两组数据是显著差异性。如果P值大于0.05说明这两组数据是非显著差异性。
6.统计学中t值p值是什么意思
1、t指的是T检验,亦称student t检验(Student's t test),主要用于样本含量较小(n计算:t的检验是双侧检验,只要T值的绝对值大于临界值就是不拒绝原假设。
2、P值(P value)就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。如果P值很小,说明原假设情况的发生的概率很小,而如果出现了,根据小概率原理,我们就有理由拒绝原假设,P值越小,我们拒绝原假设的理由越充分。
计算:概率定义为:P(A)=m/n,其中n表示该试验中所有可能出现的基本结果的总数目。m表示事件A包含的试验基本结果数。
拓展资料
统计学是关于认识客观现象总体数量特征和数量关系的科学。它是通过搜集、整理、分析统计资料,认识客观现象数量规律性的方法论科学。由于统计学的定量研究具有客观、准确和可检验的特点,所以统计方法就成为实证研究的最重要的方法,广泛适用于自然、社会、经济、科学技术各个领域的分析研究。
参考资料:搜狗百科-统计学